Algorithm之常用算法

发表于 更新于 分类于 Waline：

快速排序

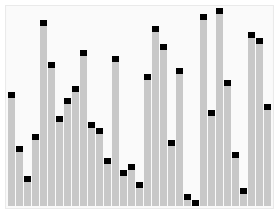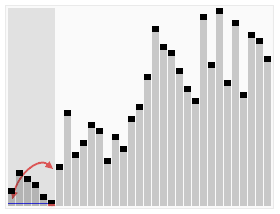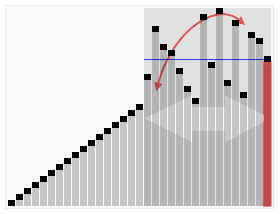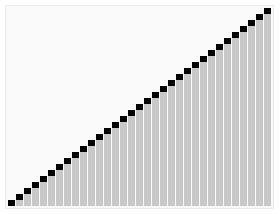
Sorting_quicksort_anim

思想

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

  1. 从数列中挑出一个元素，称为”基准”（pivot）
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
    递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

    时间复杂度

    最好时间复杂度 $O(nlog(n))$
    最坏时间复杂度 $O(n^2)$

线性时间选择

问题描述

如何找出数组A中的第 k 小的元素？ (1<=k<=n)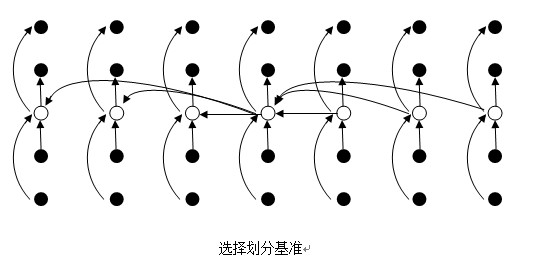
timeselect

步骤：

  1. 将n个元素分成5个一组,共ceiling(n/5)组。其中最后1组有n mod 5(余数)个元素。
  2. 用插入排序对每组排序,取其中值。若最后1组有偶数个元素,取较小得中值
  3. 递归的使用本地算法寻找ceiling(n/5)个中位数的中值x //第一次递归调用本身
  4. 用x作为划分元对数组A进行划分,并设x是第k个最小元
  5.  if i=k then return x;
 else if i<k then 找左区间的第i个最小元; //第二次递归调用本身
 else 找右区间的第i-k个最小元

流水作业调度

问题描述

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。

最优解：n个作业的加工顺序、完成n个作业所需的最短时间
最优值：T(N,0)

Johnson法则

参考

0018算法笔记——【动态规划】流水作业调度问题与Johnson法则

0-1背包问题

250px-Knapsack.svg

问题描述

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。

子问题最优值：m(i,j)
原问题最优值：m(1,c)
m(i,j)意为背包容量为j，可选择物品为,i,i+1,……,n时0,1问题的最优值。

贪心算法解

动态规划解

贪心算法

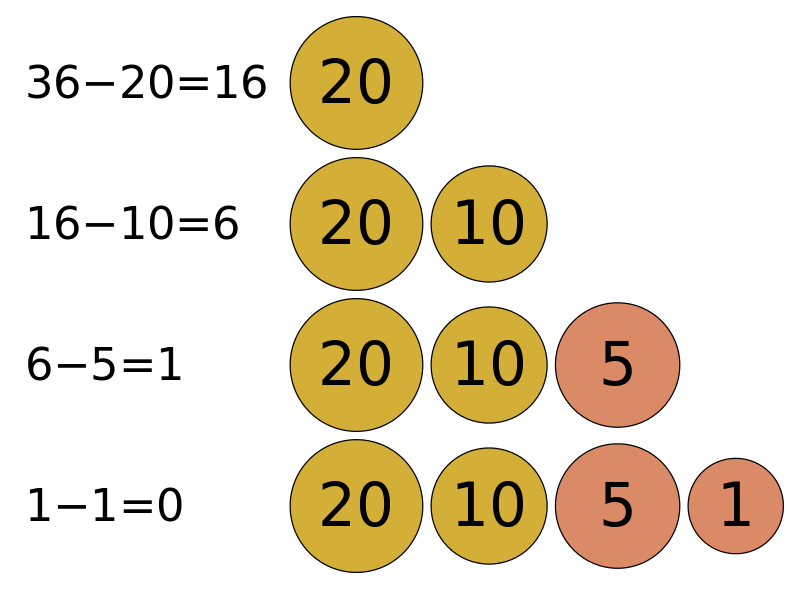
Greedy_algorithm_36_cents.svg

思想

是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。

步骤：

  1. 建立数学模型来描述问题。
  2. 把求解的问题分成若干个子问题。
  3. 对每一子问题求解，得到子问题的局部最优解。
  4. 把子问题的解局部最优解合成原来解问题的一个解。
    eg： 0-1背包问题、哈弗曼编码

    二分搜索

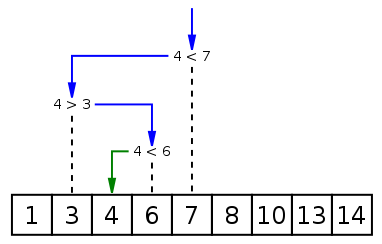
    Binary_search_into_array
    时间复杂度 $O(log(n))$
    最优时间复杂度 $O(1)$
    平均时间复杂度 $O(log(n))$

思想

一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

步骤：

给予一个包含n个带值元素的数组A或是记录A0 … An−1，使得A0 ≤ … ≤ An−1，以及目标值T，还有下列用来搜索T在A中位置的子程序[3]。

  1. 令L为0，R为n− 1。
  2. 如果L > R，则搜索以失败告终。
  3. 令m（中间值元素）为“(L + R) / 2”加上下高斯符号。
  4. 如果Am < T，令L为m + 1并回到步骤二。
  5. 如果Am > T，令R为m - 1并回到步骤二。
  6. 当Am = T，搜索结束；回传值m。
    这个迭代步骤会持续通过两个变量追踪搜索的边界。有些实际应用会在算法的最后放入相等比较，让比较循环更快，但平均而言会多一层迭代

矩阵连乘

jx

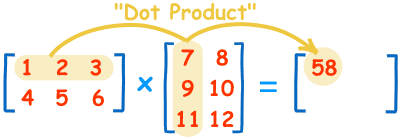
问题描述

给定n个矩阵：A1,A2,…,An，其中Ai与Ai+1是可乘的，i=1，2…，n-1。确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模，输出结果为计算矩阵连乘积的计算次序和最少数乘次数。

最优二叉搜索树

分治法

步骤：

  1. 分解：将原问题分解为若干个规模较小，相对独立，与原问题形式相同的子问题。
  2. 解决：若子问题规模较小且易于解决时，则直接解。否则，递归地解决各子问题。
  3. 合并：将各子问题的解合并为原问题的解。

eg: 快速排序

动态规划

基本思想

通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法

基本要素：

重叠子问题、最优子结构性质

试用情况

  1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
  2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
  3. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

eg: 背包问题

合并排序（归并排序）

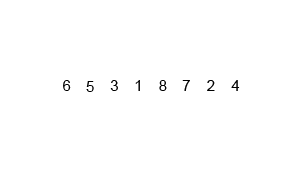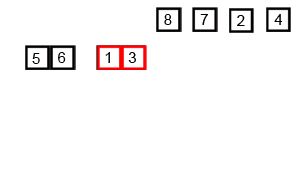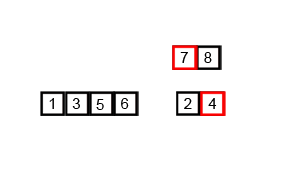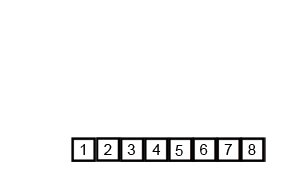
Merge-sort-example-300px
时间复杂度 $O(nlog(n))$
最优时间复杂度 $O(n)$
平均时间复杂度 $O(nlog(n))$

基本思想

将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。

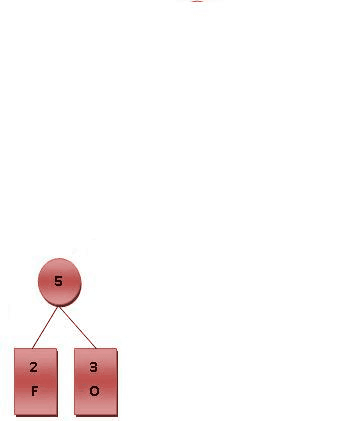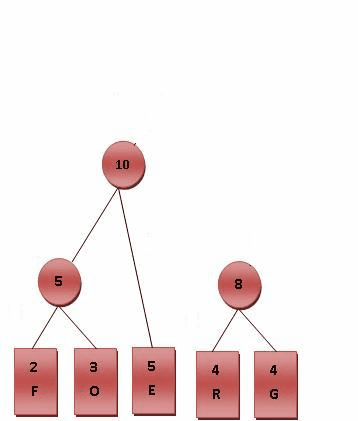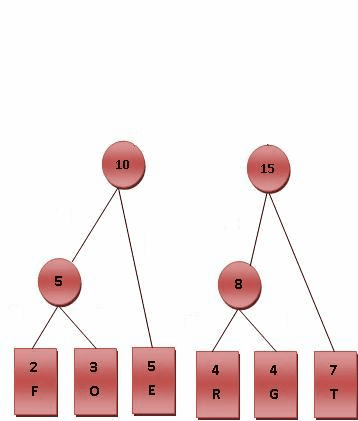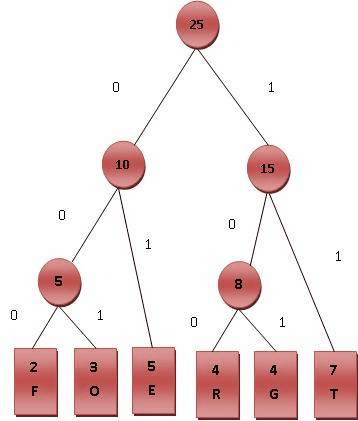
哈弗曼编码

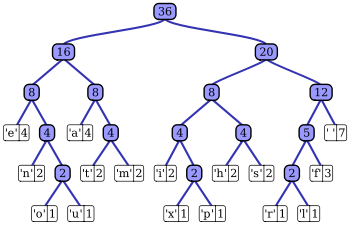
350px-Huffman_tree_2.svg
这个句子“this is an example of a huffman tree”中得到的字母频率来建构霍夫曼树。句中字母的编码和频率如图所示。编码此句子需要135 bit（不包括保存树所用的空间）

Huffman_algorithm